행렬의 소개
1. 의의
행렬대수는 연립방정식 체계로 구성된
여러 경제문제를 해결하는 데 큰 도움이 된다.
산업연관표, 선형계획법을 이해하는데 필요하며
고급경제이론 및 계량경제학에도 자주 사용된다.
2. 정의
m x n 개의 원소를 직사각형꼴로 나열해 놓은 것을 m x n 행렬이라 한다.
(원소 사이에 , 를 사용하면 안된다.)
3. 사용 예시

행렬의 계산
1.덧셈과 뺄셈
원소의 개수가 같아야 한다.

2. 스칼라곱(실수 곱)
각 원소에 실수를 곱하면 된다.
3. 곱셈
교환법칙이 성립하지 않는다. ab≠ba
참고로 벡터의 내각은 교환법칙 성립
벡터의 외적은 교환법칙 불성립이다.
2개의 행렬은 m x n n x l 처럼
앞 행렬의 열과 뒷 행렬의 행이 일치해야
계산이 가능하다.
이 때 값은 n x l 행렬로 나온다.

특이한 행렬의 종류
1.대각행렬
대각원소 이외의 모든 원소가 0인 정방형 행렬.
이때 대각선 방향은 무관하며 다 0이어도 상관없다.
두개의 대각행렬을 서로 빼거나 더하거나 곱하여도 대각행렬이 된다.

2.영행렬
모든 원소가 0인 행렬이다.
3.단위행렬 (=항등행렬)
행과열이 같으면 1 다르면 0인 행렬


4.전치행렬
A의 제 i 형을 제 j열로 바꾸어 놓은 행렬.
5. 대칭행렬
처음행렬=전치행렬을 만족시키는 행렬이다.
6.멱등행렬
A제곱 = A가 나오는 행렬.
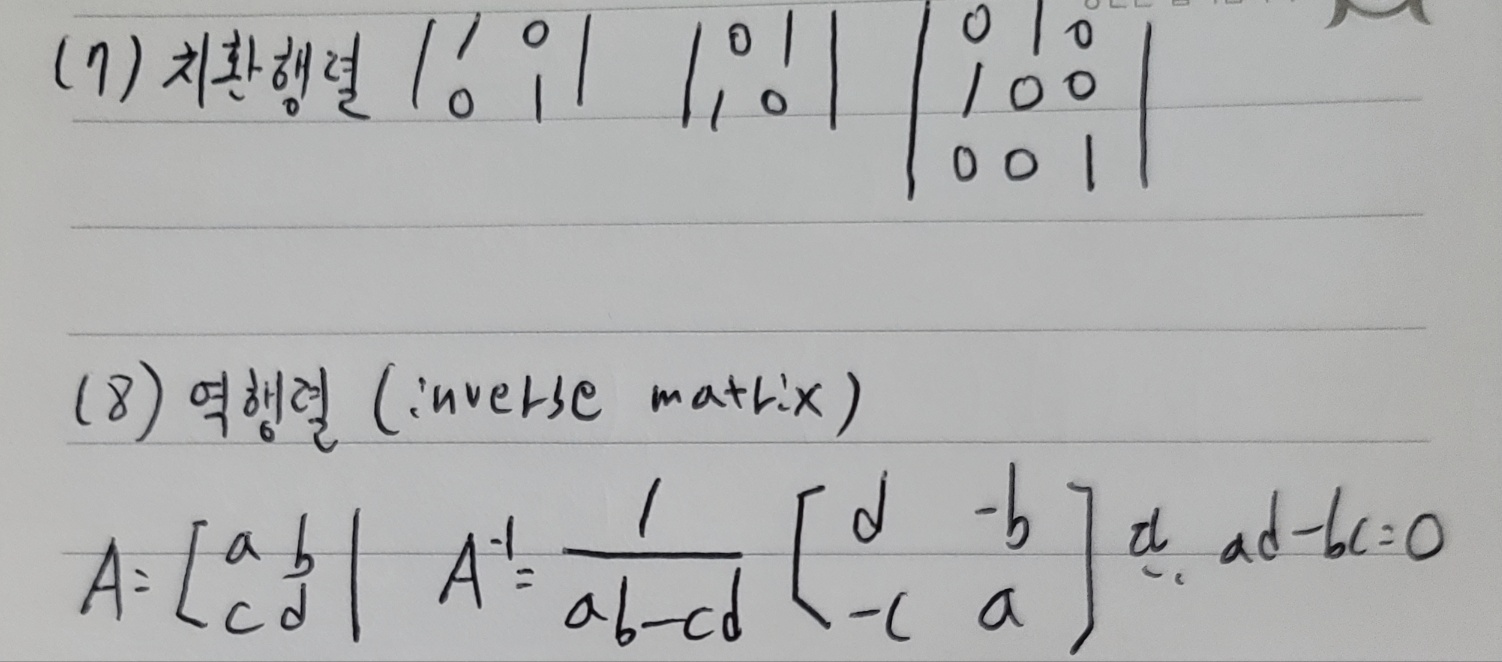
7. 치환행렬
정방행렬의 각 행과 열 중
한 원소만 1이고 나머지 원소는 0인 행렬
8. 역행렬
A가 정방행렬이고 AB=BA=I 인 행렬의 경우
B가 A의 역행렬이 된다.
'경제수학' 카테고리의 다른 글
| 대수함수의 미분법 (0) | 2023.08.16 |
|---|---|
| 4. 행렬식 (2) 행렬식의 성질과 역행렬 (0) | 2023.08.09 |
| 4. 행렬식 (1) n차 행렬, 소행렬식 여인수 (0) | 2023.05.17 |
| 2. (경제수학) 벡터 (0) | 2023.04.26 |
| 1-1 선형모형과 행렬대수 (정태분석) 행렬의 기본행연산 (0) | 2022.09.13 |



