패널 자료 정의 및 특징
횡단면 구성단위 들로 구성한 것을 시간 단위로 표현
일반적으로 Xit로 사용.
해석 (index)
Xit: 개체 i의 시간 t시점에서의 X값
예시: 소득, 나이, 경력
Xi: 개체 i의 시간 불변적 특성
예시:유전적 요소 등
Xt: t 시점에서 모집단 모든 개체에게 영향을 미치는 특성
예시: 금리 등
패널 모형 (1) 회귀 모형
(1)단일 회귀모형 : Yit = α+ Xitβ + Uit
(2) 다중 회귀모형 : Yit = α+ Xitβ + Ci + ε it
Ci = 시간 불변 고유 효과
시간에 따라 변하지 않는 부분
절편이 개개인마다 다름
(횡단면은 다 동일했다.)
외생성 (Exogeneity)
독립변수와 오차항 간의 통계적 관계
횡단면 자료에서 ZCM 조건이 대표적인 독립변수의 외생성
패널자료 모형은 오차항이 두 부분으로 나눠지므로
횡단면 자료보다 오차항과 독립변수 간의
통계적 관계에 더 유의해야 한다.
(Uit 가 Ci + ε it 로 바뀜)
강외생성 : 모든 t = 1, 2, ... , T에 대하여
E[ε it | Ci, X1i, Xi2, ..., XiT ] = 0
즉, 현재기의 오차항이 과거, 현재 ,미래 전 시점에서 독립변수와 상관관계x식으로는 Cov( ε it , Xit+1 ) = 0t기의 오차가 t+1기의 변수와 무관.
보통 대부분의 경우 성립이 어렵다.(뒤에 나올 확률 효과 모형이 버려지고고정 효과 모형이 사용되는 이유)
ex) 강 외생성이 성립한다는 것은 예를 들어
기업 i의 t시점 매출액이 Y인 경우
기업 i의 t시점 연구비 X는
기업 i의 t시점 예상못한 충격 ε (파산 등) 과 무관하다
패널 모형 (2)확률 효과 모형
E[ε it | Ci, X1i, Xi2, ..., XiT ] = 0 성립
즉, 강외생성이 성립되어야 한다.
즉, 거의 볼 일이 없다.
패널 모형 (3) 고정 효과 모형
E[ε it | Ci, X1i, Xi2, ..., XiT ] ≠ 0 여도 괜찮다.
즉, 외생성이 조금 무너져도 무방하다.
회귀식 : Yit = α+ Xitβ + Ci + ε it
고정효과 모형 추정 (1) 1계 차분 추정량
t+1기에서 t기를 빼주면
상수항이 없는 횡단면 데이터로
변환되는 원리를 이용한다.
즉, 1시점 전의 모형을
원 시점 모형에서 뺀 모형에다가
OLS를 적용하는 모형이다.
오차항이 제거되었으므로
xit와 상관관계가 있더라도 불편추정량을 얻을 수 있다.
또한 새로운 오차항 εi는
시간 개념이 없기 때문에
자기 상관이 존재하지 않는다.
다만 만약 3기 이상이 되는 경우에는
오차항 εit에 t가 생기므로
자기상관이 존재하는지 검겅해야 한다.
자기 상관이 존재하지 않아야
좋은 추정량을 구할 수 있다.

식은 위와 같다.
(간편하게 보기 위해 1기와 2기만 설정)
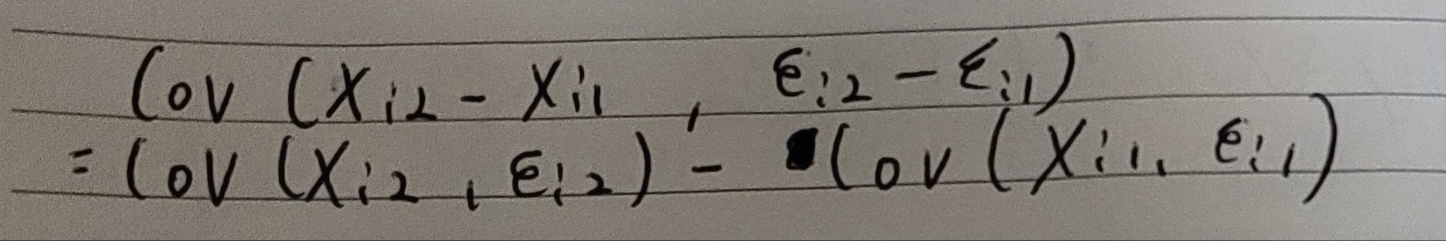
즉(Xi2 - Xi1) 와 (εi2 - εi1) 의 상관관계는
(Xi2, εi2) - (Xi1,εi1) 의 상관관계와 동일하다.
고정 효과 모형 추정 (2) 그룹 내 추정량 (within estimator)
그룹 내 추정량 (확률변수 Wit)을 사용해도
고정효과모형을 추정할 수 있다.
이 모형은 각 패널 그룹에서
시간에 걸친 평균값을 구한 후
원 모형에서 위의 평균값을 제거한 모형을
다시 뺀 모형이다.
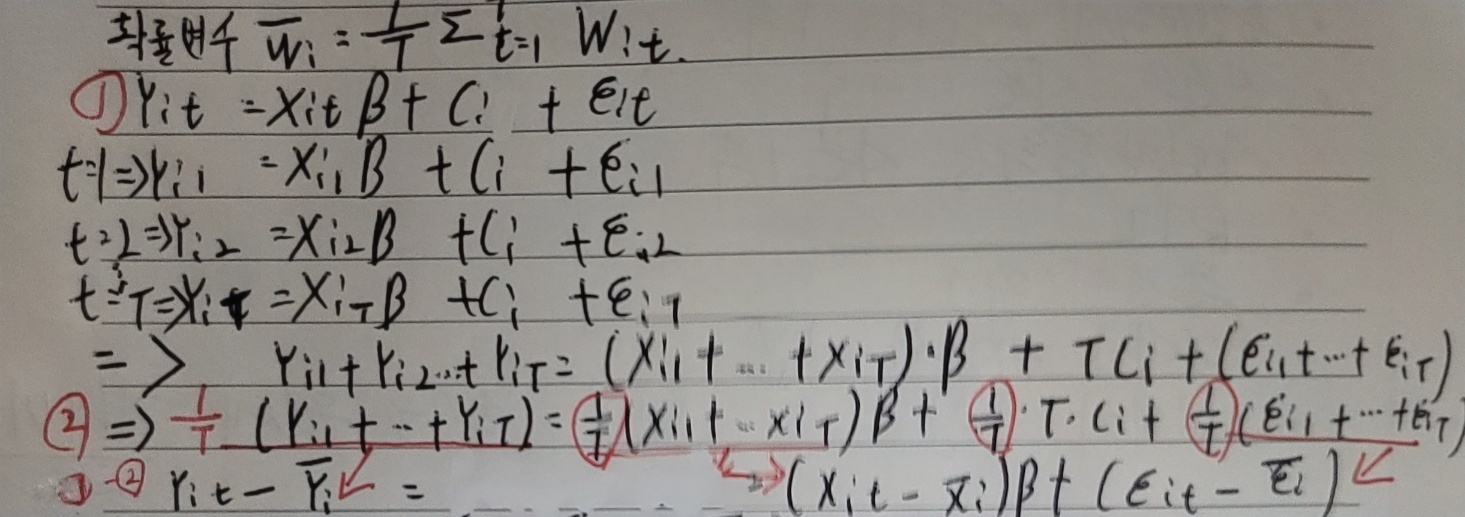
식은 위와 같다.
확률변수 wi의 슬러시 즉, wi의 추정량(평균)을
제일 위와 같이 설정한다.
고정효과 모형의 기본 회귀식은 1과 같다.
그리고 t=1 부터 T기 까지 진행 시의 식에서
확률 변수 Wit를 사용하여 추정하면
모든 식에 1/T이 적용되었기 때문에
기대값(평균)이 추정된 2의 식이 나온다.
이제 1에서 2를 빼면 마지막 식이 나온다.
위의 두 추정을 사용하면
결과적으로 고정효과 모형에서
독립 변수가 오차항과 연관이 있어도
불편 추정량을 얻을 수 있다.
단, 시간 불변하는 독립변수의 계수는
사라지기 때문에(식에서) 추정할 수 없다.
되도록 모든 시간 가변수들을 포함해야 좋다.
군집화 강건 표준오차
이분산 때와 마찬가지로 강건 표준 오차 사용을 항상 고려해야 한다.
패널 자료는 표본이 개채별로는 i.i.d(individual= 각각) 이지만
각 개체의 오차항은 시간적으로 연관되어 있을 수 있기 때문이다.
(사용법은 stata 게시판 참고)
따라서 군집화 강건 표준오차를 사용하여
에러텀들이 시간별로 연관성 있다는 걸 고려해 계산시켜야 한다.
참고로 군집화 강건 표준오차는
패널외에도 군집화 되어 있는 여러 곳에서 사용.
(ex:산업별, 위치별 등)
'통계, 계량 경제학' 카테고리의 다른 글
| 시계열자료 (0) | 2023.11.15 |
|---|---|
| 이분산 (1) | 2023.10.25 |
| 추정 (모집단 특성 추정) (0) | 2023.06.26 |
| 확률변수 (0) | 2023.06.19 |
| 자료의 정리 (0) | 2023.06.15 |
