다중회귀분석의 필요성
1)주어진 종속변수에 대한
설명력을 가지는 변수는 보통 여러 가지.
2)같은 변수라고 해도 선형이 아닐 수도 있다.
(임금은 나이에 따라 올라가다가 떨어진다.)

3)ZCM 등 단순회귀분석의 주요 가정들이
만족되지 않을 가능성이 높다.
단순회귀분석 문제의 예
<교육 지출이 학업 성적에 미치는 영향>
score i =B0+B1expen i + B2avginc i + B3children i + Ui
라는 다중함수가 있다고 생각하자
이를 단순회귀로 처리하면
score i =B0+B1expen i + Ui가 되고
오차항 Ui안에 자녀수, 수입 등등이 다 들어간다.
그리고 ZCM이 성립해야해야 하기 때문에
지출과 수입, 지출과 양육수 간에는
영향이 없어야 한다.

다중회귀분석의 특징
1)k개의 독립변수 : X1 ~ Xk 까지
2)모형 : Y=B0 + B1X1 + ... + BkXk + U(오차항)
각 각의 B들을 해석할 때
나머지 B와 U는 고정한다.
3)최소자승추정량 사용
최소자승추정량의 성질
기본적으로 단순회귀모형과 동일하다.
1. 모형 : Y=B0 + B1X1 + ... + BkXk + U(오차항)
2. 확률분포 = 랜덤 샘플링
(분산 심하면 할 때마다 값이 심하게 바뀜)
3. ZCM 가정 성립(OLS) : 각 X들은 U에 영향없다.
4. 완전공선성 있으면 안됨(추가됨)
5. 동분산 가정

-참고-
결정계수 R제곱 = ESS(SSR) / TSS(SST)
즉, Y의 총변동 중에서
X로 인해 설명되는 Y의 부분의 비율
더 자세한 사항은
https://haeul75.tistory.com/43?category=1091391
4.단순회귀분석 (1)
경제학적 모형 vs 계량 모형 경제학적 모형 : 여러 변수들에 대한 관계. 변수들은 완벽하게 관측된다. 계량모형 : 데이터 + 경제학적 모형 변수들이 모두 관측되지는 않는다. ex) wage=B0+B1 educ + B2 exp
haeul75.tistory.com
R스퀘어 (0~1 사이)가 1에 가까워지면
분산 값이 매우 커짐
완전공산성이면 R스퀘어 = 1
다중공선성 과 완전공선성
다중공선성 : 독립변수 간의 높은 상관관계
(OLS 추정량의 분산이 커짐)
완전공선성 : 두 독립변수간 상간관계 1 or -1
(OLS 추정 불가)
예를 들어 하나를 알면 하나가 정확히 예측 가능
예를들어 Y= B0+B1남성 + B2여성 + U 의 경우
(남성과 여성이 독립 변수) 돌아가지 않는다.
누락변수편의
예를 들어 어떤 변수 Xi가
1)다른 모형변수 Xj와 상관관계를 가지고
And 2) Xi가 직접 Y에 영향을 줄 때
그러한 변수 Xi를 누락하면 E[u|x]=0 가정이 위배됩니다.
(관측 혹은 측정이 어려운 경우 누락합니다.)
이 때문에 OLS 가정량에 Bias가 생기고
OLS 추정량의 Unbiasedness 가 성립하지 않게 됩니다.
이 경우 OLS 추정량에 생긴 Bias를
누락변수편의 (OVB: Omitter variable Bias) 라고 합니다.
따라서 반대로 누락변수 편의가 0이 되기 위해서는
Xi와 Xj가 상관관계가 없거나
B2= 0이 되어야 합니다.

누락변수가 발생할 때 각 변수의 추정은
위의 식과 같습니다.
∂1는 x1과 x2의 상관계수를 의미합니다.
<과다추정과 과소추정>
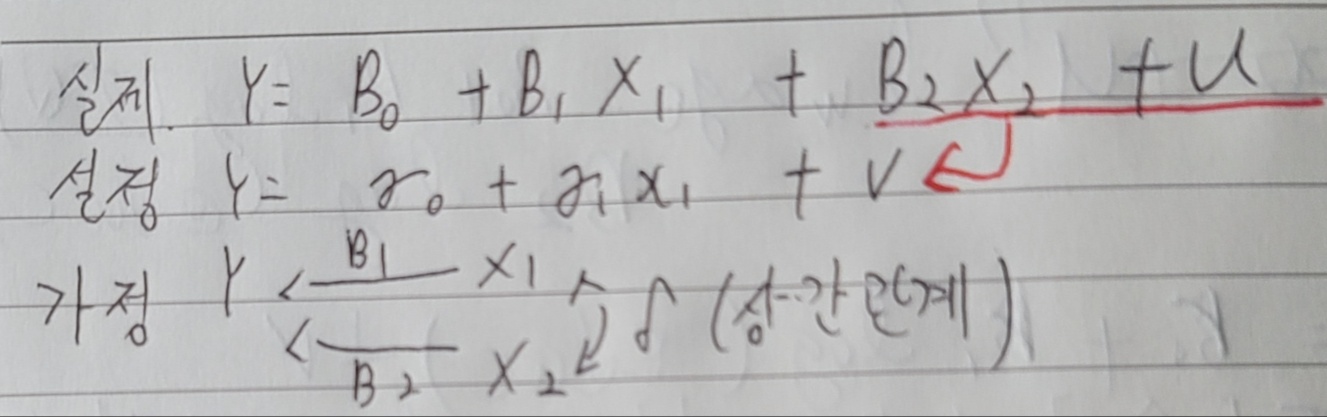
위 식에서 Y를 임금 X1을 교육 X2를 능력으로 하고
능력의 추정이 어려워 누락되었다고 가정합니다.
그리고 능력과 교육은 각각 임금에 영향을 미치며
능력과 교육 상호간에도 영향을 미칩니다.
이때 두 변수 X1, X2는 상호 양의 상관관계를 갖습니다.
즉 능력이 오르면 교육이, 교육이 오르면 능력이
증가하는 양의 관계입니다.
이 경우 r1은 X2의 누락으로
훨씬 크게 추정됩니다.
반대로 음의 관계였으면 X2의 누락으로
훨씬 적게 추정될 거고요.

이를 식으로 표현하면 아래와 같습니다.
알파 + 베타 즉, B1+B2 (위에서는 교육과 능력)은
상호 상간관계이자 각각 Y에 영향을 주므로
알파+베타의 값이 1보다 큰지 작은 지에 따라
과소추정과 과다추정이 일어나게 됩니다.
'통계, 계량 경제학' 카테고리의 다른 글
| 확률변수 (0) | 2023.06.19 |
|---|---|
| 자료의 정리 (0) | 2023.06.15 |
| 단순회귀분석 (2) (1) | 2023.04.18 |
| 4.단순회귀분석 (1) (0) | 2023.04.10 |
| 3. 추정과 검정 (0) | 2023.03.29 |


